Logical equivalence

In logic, statements p and q are logically equivalent if they have the same logical content.

Syntactically, p and q are equivalent if each can be proved from the other. Semantically, p and q are equivalent if they have the same truth value in every model.

The logical equivalence of p and q is sometimes expressed as 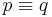p \equiv q, Epq, or 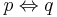p \Leftrightarrow q. However, these symbols are also used for material equivalence; the proper interpretation depends on the context. Logical equivalence is different from material equivalence, although the two concepts are closely related.

Example

The following statements are logically equivalent:

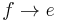  1. If Lisa is in France, then she is in Europe. (In symbols, f \rightarrow e.)
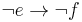  2. If Lisa is not in Europe, then she is not in France. (In symbols, \neg e \rightarrow \neg f.)

Syntactically, (1) and (2) are derivable from each other via the rules of contraposition and double negation. Semantically, (1) and (2) are true in exactly the same models (interpretations, valuations); namely, those in which either Lisa is in France is false or Lisa is in Europe is true.

(Note that in this example classical logic is assumed. Some non-classical logics do not deem (1) and (2) logically equivalent.)

Relation to material equivalence

Logical equivalence is different from material equivalence. The material equivalence of p and q (often written p↔q) is itself another statement in same object language as p and q, which expresses the idea "p if and only if q". In particular, the truth value of p↔q can change from one model to another.

The claim that two formulas are logically equivalent is a statement in the metalanguage, expressing a relationship between two statements p and q. The claim that p and q are semantically equivalent does not depend on any particular model; it says that in every possible model, p will have the same truth value as q. The claim that p and q are syntactically equivalent does not depend on models at all; it states that there is a deduction of q from p and a deduction of p from q.

There is a close relationship between material equivalence and logical equivalence. Formulas p and q are syntactically equivalent if and only if p↔q is a theorem, while p and q are semantically equivalent if and only if p↔q is true in every model (that is, p↔q is logically valid).

See also